Direct-Address-Search(T,k)
		return(T[k]);

	Direct-Address-Insert(T,x)
		T[key[x]] = x;

	Direct-Address-Delete(T,x)
		T[key[x]] = NULL;

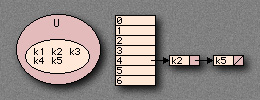
If |U| is very large, storing such a table (T) is impossible. On the other hand, the set K of keys actually stored may be small and most of the space allocated for T would be wasted.

The Hash Table

With direct addressing, an element is stored in slot K. With hashing, it is stored in slot H(k). H() is called the hash-function. H maps the universe (U) of keys into the slots of a hash-table (T[0 ... m-1]).

	h: U = {0, 1, 2 ... m-1}

An element with key K hashes into slot H(k), also, H(k) is the hash value of key K.

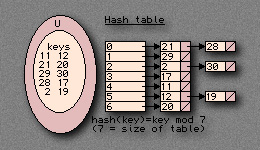
The hash functions is as follows: H(k) = k mod SIZE_OF_TABLE

Collision Resolution by Chaining

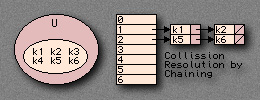
	Chained-Hash-Insert(T,x)
		insert x at the head of the list T[h(key[x])];
		// Worst Case: O(n)
	Chained-Hash-Search(T,k)
		search for an element with a key K in list T[h(k)];
		// Worst Case: O(length of list T[h(k)];
		// Usually O(1)
	Chained-Hash-Delete(T,x)
		delete X from the list T[h(key[x])];
		// Roughly O(n) time

Folding

A key is divided into several parts. These parts are combined or folded together and are transformed in a certain way to create the target address (index of hash-table).

Shift Folding

Here is an example of what I mean by folding. Let's take a common item: A social insurance number. It is made up of 9 digits, grouped in 3 sets of 3 digits.

	123 456 789

We then break down this 9 digit number into it's parts, sum them and then mod it by the size of the table (in this example, the table size is 1000)

	 123
	 456
	+789
	1368 mod 1000 = 368

Notes:

Assume that any given element is equally likely to hash into any one of the m's slots (Simple Uniform Hashing).

Let |T| = M_t, and we have n elements to be stored in T. We define the load factor L=n/m.

Certainly, the worst case of hashing is 0(n).

Theorem 1

In a hash table where collisions are resolved by chaining, an unsuccessful search takes Big-Sigma (1+Load Factor) time, under the assumption of uniform hashing.

Proof

A key is equally likely to hash into any of the M slots. The average time to search unsuccessfully for a key is the average time it takes to search to the end of a linked list. The average length of the list is exactly the Load Factor (L=n/m). Therefore, the expected number of elements examined in an unsuccessful search is L and the total time is L+1, including the time to compute H(k).

Theorem 2

In a hash table in which collisions are resolved by chaining, a successful search takes O(1+Load Factor) time. Assuming, of course, we have Simple Uniform Hashing.

To make this proof easier to understand, I am assuming that the CHAINED-HASH-INSERT() function inserts a new element at the end of the list instead of at the front. (*NB In theory, there is no difference. Some people like it this way.)

Proof

You have to assume that the key being searched for is equally likely to be any of the N keys stored in the table. The expected number of elements inspected during a successful search is 1 more than the length of the list when the sought-for element was inserted.

To find the expected number of elements examined, you take the average over N items in the of 1+the expected length of the linked list to which the I'th element was added. The expected length of the list is (i-1)/m.

And, of course, here is the solution:

1+(n/2m)-(1/2m) = 1+(Load Factor/2)-(1/2m) = O(1+Load Factor)
Therefore, the total amount of time required for a successful search is:
1+(Load Factor/2)-(1/2m) = 2+(Load Factor/2) - (1/2m) = O(1+Load Factor)

Good Hash Functions

A hash function that causes NO collisions is called a Perfect Hash Function and a Good Hash Function is one that satisfies Simple Uniform Hashing.

Guidelines for simple uniform hashing

Assume all keys are natural numbers.

	1. H(k) = k mod m
	2. m should be a prime number close to some power of 2

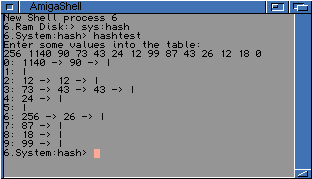
A working example of a hash table

The following is an example of a hash table with Simple Uniform Hashing. It uses a Linked List to resolve collissions. The example souce code is included. Although developed on a Commodore Amiga, it will compile and run under Windows 95 or 98. You need to compile linklist.cpp and hashtable.cpp without linking it, then compile hashtest.cpp and link it with linklist.obj and hashtable.obj.

Sample output of hashtest.

LinkList.cpp
HashTable.cpp
HashTest.cpp

And there you have it, a simple guide for Hashing. I hope you have had as much fun as I have with this. May all your days of making databases ect ... be happy ones. Thanks to Dr. Zhu for the informaitve lecture.